Nous avons vu dans les articles précédents le fonctionnement des signaux et les niveaux en acoustique.
- La sensation sonore (d’intensité en dB ou fréquentiel en Hz) varie comme le logarithme de l’excitation.
- Le dB est un rapport sans dimension (rapport de puissance mais aussi rapport de tension ou d’intensité sonore...).
- Le dB adopte l’échelle logarithmique.
- le seuil d'audition (I0 = 10-12 w / m2) de l'oreille qui est la plus petite intensité acoustique à 1KHz décelable à l'oreille.
- Le tympan est un capteur de pression (micro omni) de ≈ 1 cm de diamètre (donc sensible aux variations de pression).
Nous avons parlé du Bel et de sa sous-unité le décibel acoustique que l'on mesure en SPL (Sound Pressure Level). Voici une illustration qui explique les différents niveaux sonores dans notre quotidien :
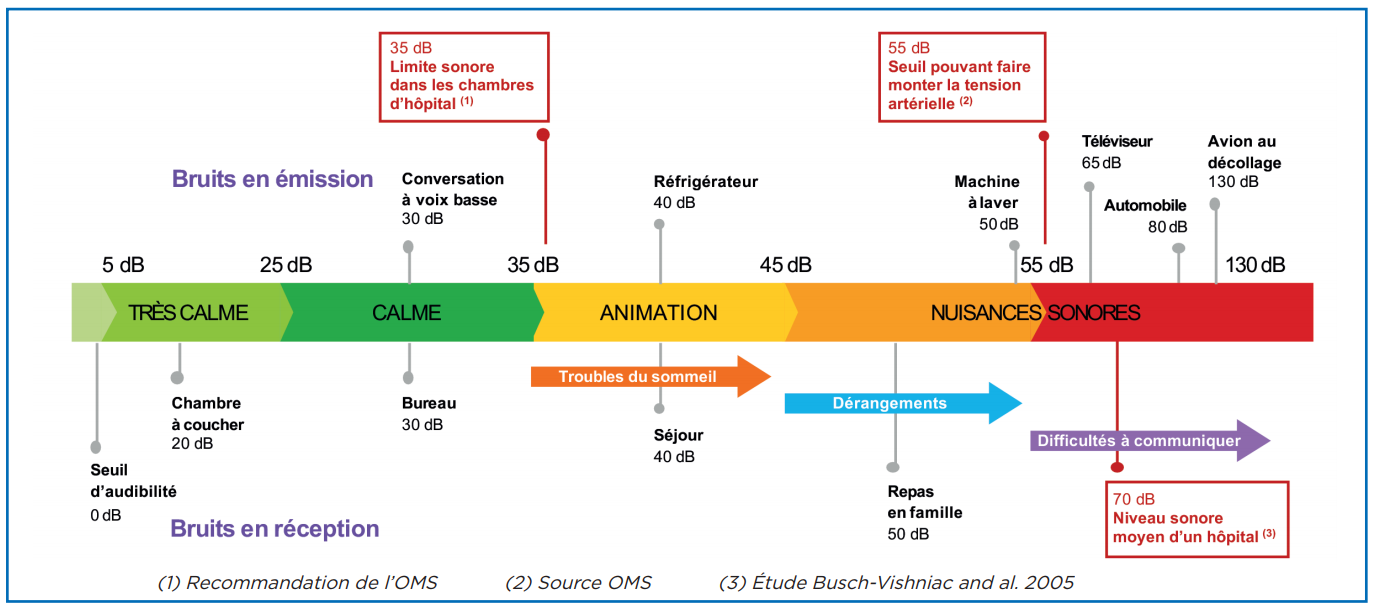
Notez qu'aux alentours des 80 90 dbspl nos avons un muscle, le stapédien qui en se contractant permette de protéger l'oreille en cas de fort exposition.
A titre indicatif le volume moyen pendant une seance studio qui peut avoisiner les 80, 85 dbspl
L'oreille humaine
Voici comment se compose notre oreille :
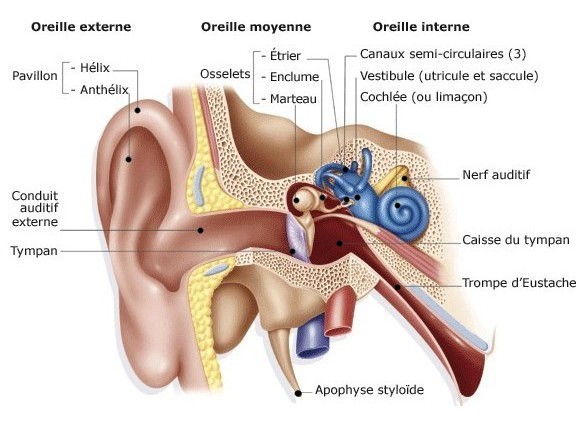
Ce qui est intérressant en dehors du tympan et du conduit auditif, vous avez la cochlée avec une petite mebranne qui l'on appelle la menbrane basilière dans laquelle se trouve des cellules ciliées qui qonr relièes a des nerfs auditifs qui sont reliées au cerveau. La répartition logarithmiques des cellules ciliées provoque une meilleure discrimination dans le grave que dans l’aigu.
Ces cellules agissent un peu comme un analyseur de spectre car car chaque cellule vont être accordés à certaines fréquences toujours de manière logarythmique. Ce qui veut dire que nous avons plus de cellules dans le grave que dans l'aigu. Nous en possédons environ 20000. L’impression d’équilibre tonal est donc liée à cette répartition.
Cela pour conséquence de provoquer une meilleure discrimination dans le grave que dans l’aigu, c'est à dire que our une fréquence a 100 et 120 Hz notre oreille sera capable de les distinguer l'une de l'autre. C’est le pouvoir séparateur de l’oreille entre 2 fréquences.
Alors que pour des fréquences aigus comme par exemple 10000 et 10020 hz avec le même écart de fréquences, nous ne pourrons pas entendre la différence car ca sera la même cellule ciliée qui sera concerné.
Notre impression d’équilibre tonal est donc liée à cette répartition. Le meilleur exemple pour illustrer ce phénomène sont le bruit rose et le bruit blanc.
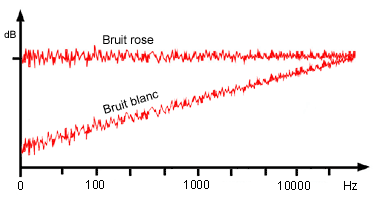
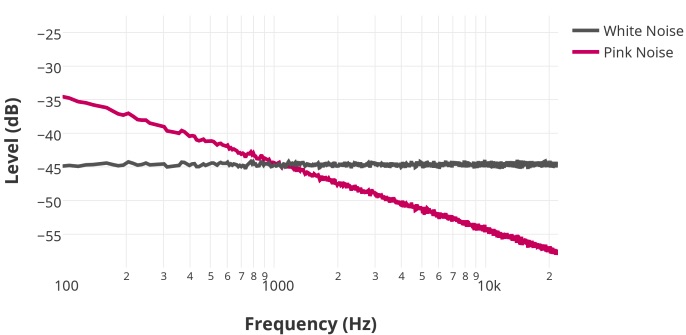
Le bruit rose vous donnera à l'oreille la sensation d'avoir autant de fréquences graves que de fréquences aigus alors qu'en réalité un bruit rose contient beaucoup plus d'énergie dans le grave. Sur une echelle logarythmique, la courbe sera plate.
Le bruit blanc contient la même quantité d'énergie a toutes les fréquences et on constate que la courbe va en crescendo. A l'oreille on sera plus sensible aux fréquences aigus.
Avec une échelle lineaire on constate que la courbe du bruit rose contient plus de grave que d'aigu et que celle du bruit blanc est parfaitement equilibré.
Notre oreille fonctionne de manière logarythmique en niveau, c'est pour ça que nous avons inventé une unité logarythmique le dB qui est avant tout une unité physiologique. Nous travaillons de manière linéaire pour les fréquences mais on les représente avec une echelle logarythmique pour des questions de visualisations par rapport à ce qu'on entend. Cela explique aussi pourquoi les octaves existe en musique car ils sont liée a cette répartition de ces fréquences.
Les courbes d’isosonie
Isononie éthymologiquement parlant signifie égales sensations sonores. On parle aussi de la courbe de phon.
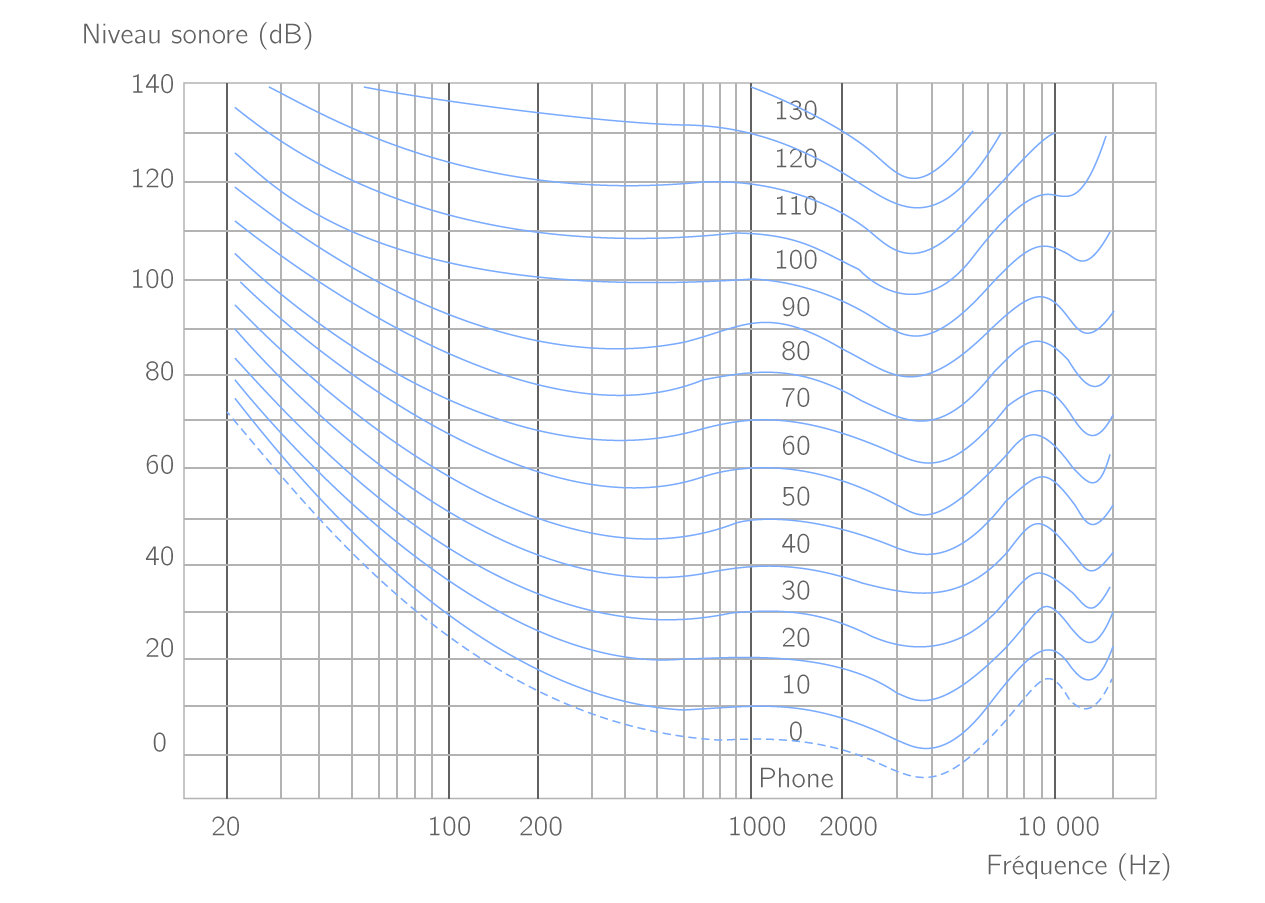
Pour comprendre cette courbe, vous pouvez regarder la fréquence de 1000 hz, on constate que nous sommes capable d'entendre cette fréquence à n'importe quel volume. En revanche pour les fréquences grave, on constate qu'il faudra beaucoup plus d'énergie pour pouvoir avoir le même sensation de niveau.
Par exemple si vous écoutez un son à 60 db et que vous souhaitez ressentir autant de 1000 hz que de 40 hz, il faudra augmenter la fréquence de 40 hz d'environ 30 db. Si vous réalisez un mixage à ce niveau de 60 db, pour que balance tonal soit équilibré, "psychoacoustiquement" vous allez mettre plus de grave que de médiums aigus.
Vous allez réaliser un mix qui va s'adapter à une écoute de faible niveau, si vous jugez que d'un point de vue artistique cela vous convient. Mais lorsque vous allez l'ecouter à 80 ou 90 db, vous n'allez pas retrouver votre équilibre tonal de base.
Voilà pourquoi il faut absolument aligner vos niveaux d'écoute lors de vos mixages et les adapter à votre circuit de production.
Faites l'expérience d'écouter un mixage avec une bonne balance tonal et de faire des écoutes comparatives en baissant le niveau du mix sans modifier votre niveau d'écoute. Pour rappel la norme ITU recommande un niveau d'écoute "musique" de 79 db(c). (La courbe de pondération C est quasiment linéaire).
Prennons un autre exemple d'un point de vue electrique : prenons ce même son de 1000 Hz à 60 db avec un ampli 1w électrique. Si on change sa fréquence à 30 Hz, nous avons besoin de 30 db de niveau supplémentaire, on multiplie par 10 la puissance par augmenter de 10 db (1bel) soit 10(3), il nous faudra donc un ampli d'une puissance de 1000w pour les fournir. Souvenez vous la fonction "loudness" de nos bonnes vieilles chaine hifi qui servait précisement à combler le manque de grave à bas volume.
Autre remarque sur cette courbe c'est notre perception des fréquences entre 3 et 5 khz. quand on parlait de notre seuil d'audition qui est de 2x10-5 Pa (la quantité minimal de pression décelable à l'oreille) cette valeur est valable à 1000 hz mais on constate qu'entre 3 et 5 khz la courbe (pointillé) descend en dessous de 0.
Les courbes de pondération
Nous avions évoqué dans le début de ce dossier la différence entre un son et un bruit. Ce que nous voulons entendre sont les sons et non les bruits. Pour reprendre les courbes d'isosonie, nous allons les appliquer sur les sons et nous utilisons les courbes de pondération pour les bruits.
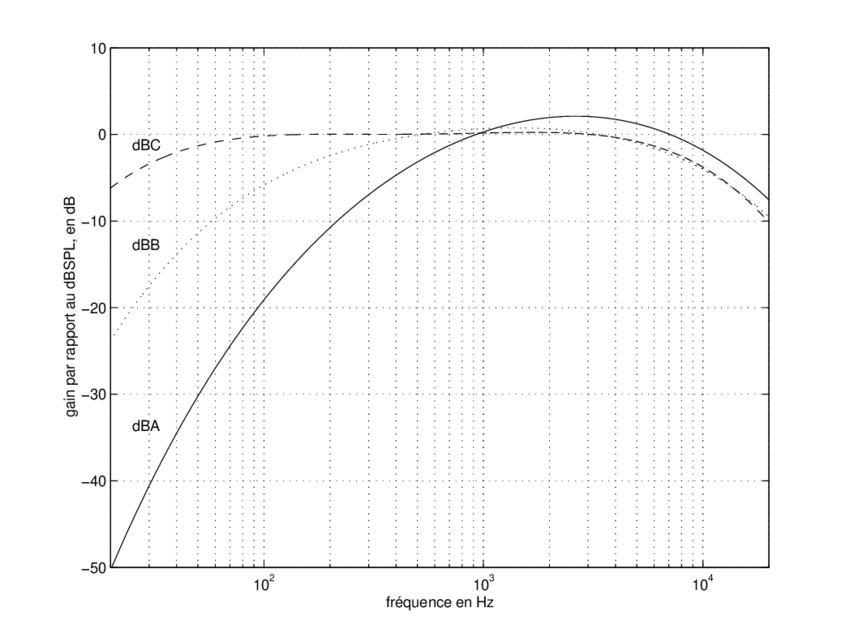
Les sonomètres certifiés permettent les mesures de bruit avec une pondération en fréquence A, C et parfois d'autres.
Ce que les humains sont physiquement capables d'entendre est représenté par la courbe de pondération A. Les sons acoustiques contiennent plus de basses et de hautes fréquences que ce que les humains perçoivent.
La courbe de pondération C représente ce que les humains entendent lorsque le son est augmenté ; nous devenons plus sensibles aux basses fréquences. Les pondérations A et C sont donc les plus significatives pour décrire la réponse en fréquence de l'oreille humaine aux sons du monde réel.
Imaginons que vous êtes en train de travailler dans votre studio et que vous êtes dérangés par du bruit à l'extérieur et que vous souhaitiez mesurer ce bruit. C'est là qu'intervienne les coubes de pondération. Notre oreille est capable de rejecter les bruits si on ne les écoutes pas particulièrement dans le grave. Si on y prete attention ces fréquences nous paraitrons plus présentes alors que si on n'y fait pas attention nous serons tout à fait capable de les rejecter.
Si vous mesurez un son avec un sonométre en appliquant une courbe de ponderation A, c'est comme si vous attenuez les composantes grave un peu comme si vous mesurez votre bruit sans y faire attention.
Comme les mesures acoustiques du niveau sonore sont souvent motivées par l'effet des sons sur l'homme, le filtre de pondération A est couramment utilisé. Le filtre de pondération C est souvent appliqué lorsqu'il s'agit de représenter les niveaux maximum.
Ces courbes s'applique en fonction du niveau SPL du bruit mesuré. Ces niveaux se déterminent en dBA, dBB ou dBC :
- Pondération A : 20 à 55 dB
- Pondération B : 55 à 85 dB
- Pondération C : 85 à 140 dB





