#4 - Décibel acoustique, mesures des niveaux

Les niveaux acoustiques

La sensation sonore est la caractéristique perceptive du son, qui est directement liée au concept d’intensité, c’est à dire la manière dont l’oreille perçoit l’intensité. En 1860 Fechner a dit : ce n'est pas la variation de pression acoustique dans l'absolu qui importe, mais la variation relative entre deux sons. La sensation de niveau sonore est lié au "Bel". Le bel peut se représenter mathématiquement par la formule suivante :

S_(Bel) = 10 log (I_a/I₀)

S = sensation sonore en Bel. Le Bel est le logarithme de (I_a) l'intensité acoustique (watts / m²) sur (I₀) le seuil d'audition (10^-12 watts / m²) de l'oreille, qui est la plus petite intensité acoustique décelable à l'oreille à 1khz.

I_a / I₀ est un rapport et lorsque l'on fait le logarithme d'un rapport, par définition on mesure une unité qui est ici le Bel (B). Le Bel est une unité physiologique et non physique adaptée à notre audition. Lorsque l'on augmente le niveau de 1 Bel on obtient le double de sensation sonore.

Notre oreille fonctionne de manière logarithmique comme représenté sur ce graphique, qui montre que la sensation de niveau sonore est proportionnelle au logarithme de l’excitation (loi de Gustav Fechner 1801-1887) :

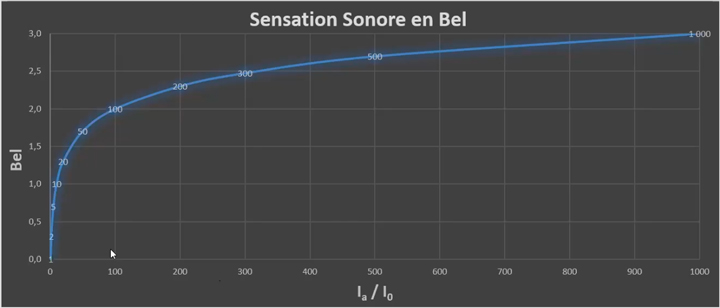
Si on démarre cette échelle par rapport à notre seuil d'audition, on dira que I_a = I₀ c'est a dire que l'intensité acoustique (qui est une évolution) est égale à notre seuil d'audition (qui est une constante) soit 1.

À ce stade, lorsque l'on commence à entendre un son, on dira que nous serons à 0 Bel. D'un point de vue mathématique : Log10 de 1 = 0.

De manière logarithmique, l'augmentation progressive de l'intensité acoustique correspondra par exemple a : log10 de 10 = 1, Log10 de 100 = 2, log10 de 1000 = 3 etc...

Pour comprendre ce principe d'un point de vue auditif, il faut multiplier par 10 l'intensité acoustique (la source sonore) pour avoir le double de sensation sonore à l'oreille. Notre sensation sonore ne varie pas comme la croissance directe de l'énergie mais au logarithme de cette croissance. D'où la nécessité des logs pour les formules mathématiques.

Niveau d'intensité acoustique (L_I) en db

C'est la perception du volume du son par l'oreille humaine. On détermine le niveau d'intensité acoustique non pas en Bel mais la sous-unité qui est le décibel. Dans un Bel il y a 10 décibels. Pour doubler la sensation de niveau sonore, nous augmenterons le niveau de 10 dB soit 1 Bel.

Pour calculer le niveau d'intensité acoustique, nous appliquerons cette formule :

L_I= 10 log (I_a/I_o)

L_I s'exprimera en dB et I_a s'exprimera en watt/m² (à l'endroit où l'on fait la mesure) et I_o seuil d'audibilité 10^-12 W/m².

Niveau de pression acoustique (Lp) en dbSPL

En combinant la formule qui sert à mesurer le niveau d'intensité acoustique en db (L_I), nous pouvons calculer aussi le niveau de pression acoustique. Nos oreilles, qui sont des capteurs de pression purs, entendent uniquement de la pression. Ne pas confondre avec l'énergie sonore globale, qui est l'intensité acoustique, et la pression acoustique, qui n'est qu'une partie de cette énergie.

Pour éviter toute confusion, il existe des formules mathématiques qui permettent de faire la distinction entre le niveau d'intensité acoustique (watts/m²) et le niveau de pression acoustique, qui lui s'exprime en dBSPL (Sound Pressure Level).

Dans l'air (quand on est loin de la source et en champ libre) il y a une relation entre l'impédance acoustique (Za) et la pression acoustique (p).

L'impédance acoustique fonctionne comme une résistance au passage du son (un peu comme si on empêchait nos molécules d'air de transmettre les vibrations), c'est ce que l'on fait avec du traitement acoustique par exemple.

Il y a une relation entre la pression acoustique, l'intensité acoustique et l'impédance acoustique (Za) de l'environnement dans lequel se déplace le son, donc dans l'air, est égal à environ 410 ohms_a (ou Rayls) en champ libre.

I_a = p² / Za

À partir du moment où l'on connaît le niveau de pression acoustique, que l'on peut mesurer à l'aide d'un sonomètre par exemple, il est possible, grâce à ce calcul, de déterminer l'intensité acoustique, qui est plus représentative de ce que l'on entend.

Si on applique la formule sur le niveau d'intensité acoustique (L_I) L_I= 10 log (I_a/I_o) pour mesurer L_p (le niveau de pression acoustique en dBSPL) cela nous donne :

L_I = 10 log ((P²/ZA)/I0)

(On applique la règle des logs : Log p² = 2log p)

L_p = 20 log (p/p0)

(p en Pascal et p₀ étant la plus petite pression acoustique décelable à l'oreille à 1000Hz qui correspond à I₀ qui est de 2 . 10^-5 Pascal).

Pour faire simple, si vous mesurez avec un sonomètre le niveau de pression en dBSPL en champ libre vous serez égal au niveau d'intensité acoustique. (L_i = L_p). Ces valeurs vont changer en fonction de l'acoustique d'une salle et de l'endroit ou l'on va mesurer. Contre un mur par exemple vous aurez plus de niveau de pression mais avec une intensité acoustique différente car l'impédance acoustique va varier.

Niveau de puissance acoustique (L_w)

On peut mesurer la puissance acoustique d'une source en Watts acoustique (W_a). La puissance acoustique correspond à l'ensemble de la source sonore qui émet un son autour d'elle. Il faut en capter une partie à un endroit donné pour déterminer en db le niveau de puissance acoustique.

Nous avons vu précédemment qu'une source sonore va rayonner sur une surface donnée autour d'elle.

Pour déterminer cette puissance acoustique on peut appliquer la formule :

L_w = 10 log (W_a / W₀)

L_w en dB, W_a en Watts et W₀ = 10^-12 W)

W₀ qui est une puissance de référence.

Additions des niveaux sonores

Sources éloignées d > λ / 2 non corrélées.

Prenons 2 enceintes relativement éloignées l'une de l'autre qui généreraient 2 signaux différents mais avec la même intensité acoustique. Dans ce cas là, c'est l'intensité acoustique (l'énergie globale) qui va s'additionner (L).

Si I1 = I2 = Ia alors L = 10 log (2 I_a / I₀) = (10 log I_a / I₀) + (10 log2) = LI_a + 3dB

I1 et I2 sont nos enceintes acoustiques.

Pour résumer simplement avec 2 sources distinctes I1 et 12 il suffit de multiplier l'intensité acoustique par 2 ce qui donne 3 db.

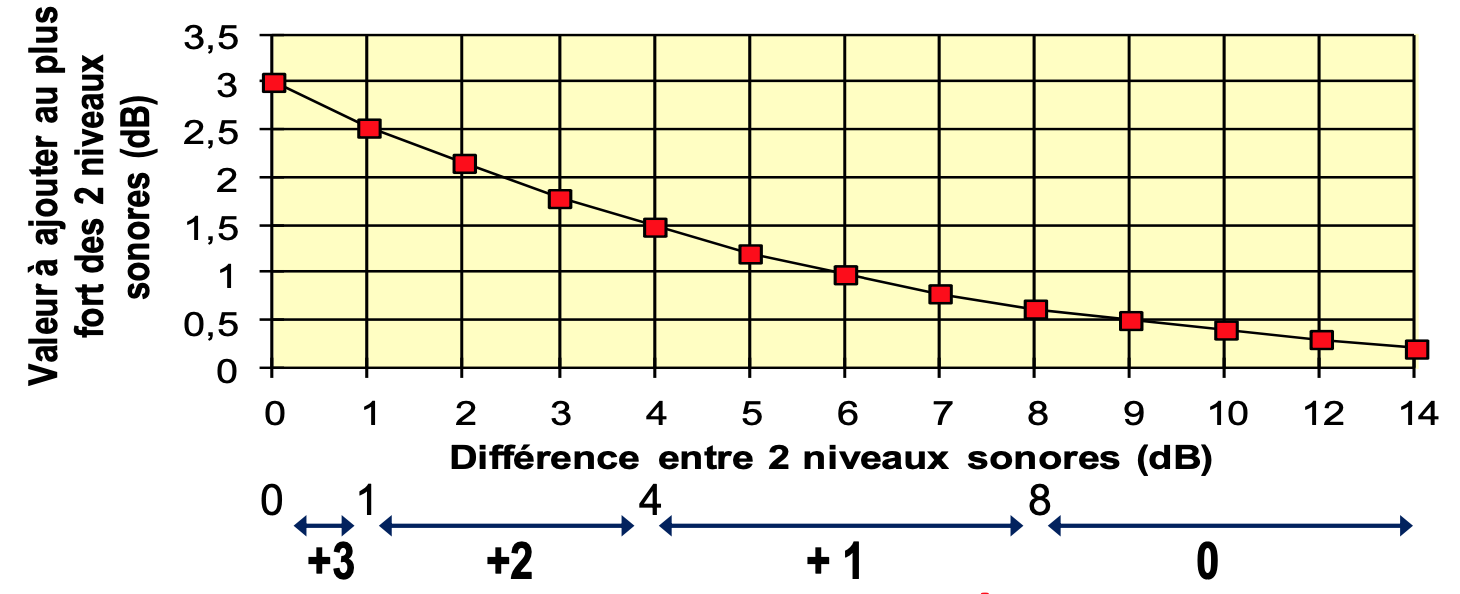
Voici un abaque qui permet d'identifier les niveaux ajoutés selon les différences de niveaux entre 2 signaux. Ce phénomène se produit lorsque vous additionnez des pistes sur une table de mixage par exemple ou avec plusieurs instruments de musique dans une salle comme plusieurs violons pour équilibrer un violoncelle.

2 sources proches λ / 2 ET corrélées.

Prenons nos 2 enceintes en les plaçant proches l'une de l'autre. Dans ce cas ce ne sera plus l'intensité acoustique mais leur pressions acoustiques qui s'additionnent.

Si p1 = p2 = p alors Lpt = 20 log (2p/p0)

Comme nous l'avons vu la pression acoustique étant non pas 10 log de 2 mais 20 log p donc au lieu d'avoir 3 db nous aurons 6 db c'est ce qu'on appelle le couplage des sources. Principe très connues en sonorisation. Par exemple pour gagner en rendement sur des fréquences à 100 hz : la moitié de la longueur d'onde et de 1,70 donc vous pouvez placer des subs très proches pour gagner en niveau.