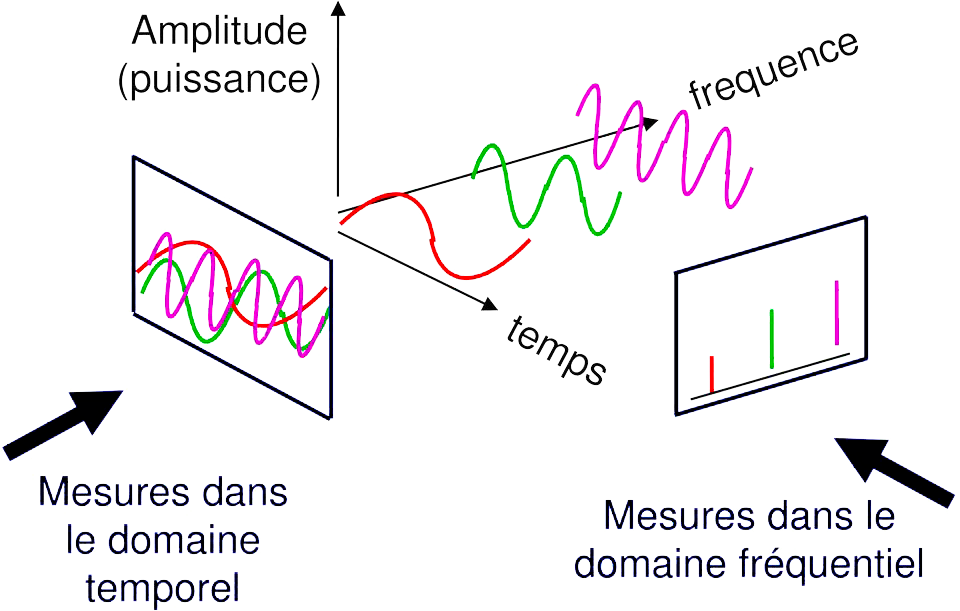
Il existe deux façon d'analyser un son, du moins nous pouvons l'observer sous 2 points de vue différents. L'analyse temporelle, où l'on observe le comportement du signal en fonction du temps, et l'analyse fréquentielle où la variable de contrôle est la fréquence.
Voici une sinusoïde analysée d'un point de vue temporel et fréquentiel.

Dans l'analyse temporelle, l'axe des ordonnées représente l'amplitude, qui peut correspondre à la pression acoustique ou à une tension, tandis que l'axe des abscisses représente le temps, généralement exprimé en millisecondes pour une mesure précise. Dans l'analyse fréquentielle, l'axe des ordonnées représente également le niveau, mais l'axe des abscisses indique les fréquences. La représentation des sinusoïdes composant le signal est appelée le spectre.
Si on prend le signal sinusoïdal, vous allez avoir une seule fréquence fondamentale F. Il s'agit d'un signal pur, sa période correspond à une seule fréquence.
Voici un autre signal avec une forme carrée :

Vous avez également une période, mais ce signal contient plusieurs fréquences, notamment la fondamentale F et les harmoniques impairs 3, 5, 7, etc. On parle ici d'un son harmonique avec un spectre de raies. Un spectre de raies respecte les rapports temporels entre les fréquences, qui correspond à un rapport de phase. On parle de fréquences discrètes qui sont distribuées de manière précises en fonction de la fréquence.
Sur un signal périodique quelconque très erratique, qui peut correspondre à n'importe quel son, vous obtenez un spectre plus complexe.
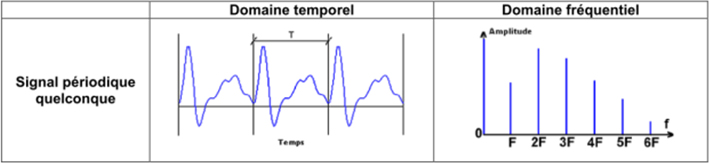
Imaginons un bruit rose, vous obtiendrez un spectre continu.
Le domaine fréquentiel et le domaine temporel
Les sons complexes harmoniques ou périodiques
Décomposition en série de Fourier
Tout ce que l'on peut faire en terme de traitement de signal au quotidien sont basé sur les travaux de M. Joseph Fourier. Il a déterminé que toute fonction périodique (qui peut en tous cas se mesurer sur une période relativement longue) peut se décomposer en une somme d’oscillations sinusoïdales (ou ondes simples). Cette somme (de fréquences fondamentales ou sons purs) est appelée série de Fourier.
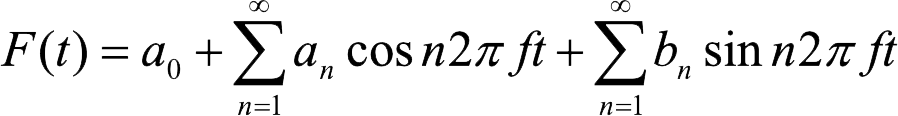
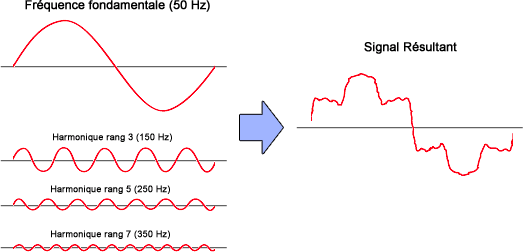
Prenons l'exemple de 2 fréquences fondamentales que l'on superpose l'une à l'autre : on obtient une autre forme de sinusoïde.
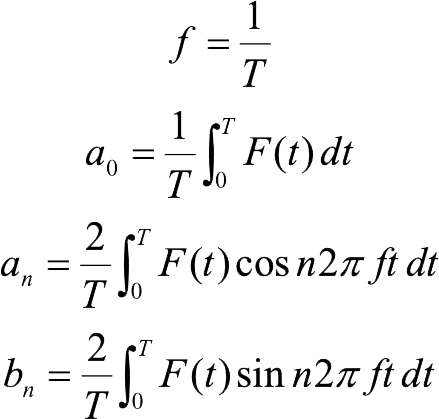
Les sons complexes apériodiques : décomposition de Fourier continue
Il existe également des fonctions non périodiques, comme par exemple lorsque que le marteau frappe la corde d'un piano. Dans ce cas, cette fonction non périodique peut s’exprimer comme une superposition continue de Fourier de la forme générale :
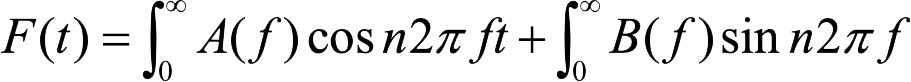
Cela signifie que n'importe quelle fonction plus complexe quelle qu'elle soit peut être décomposée sous la forme de fonction sinusoïdale sur un temps de mesure bien précis. C'est juste la formule mathématique qui change.
Les fonctions A(f) et B(f) sont appelées les coefficients de Fourier.
Un graphe donnant les coefficients de Fourier en fonction de f est appelé le spectre de fréquence de la superposition de Fourier. Tous les spectres que nous avons l'habitude de voir sur nos analyseurs sont issus de cette formule mathématique.
Voici la représentation d'une composante harmonique d'un signal pur avec une fréquence plutôt grave : amplitude en fonction des fréquences avec le fameux spectre de raies.
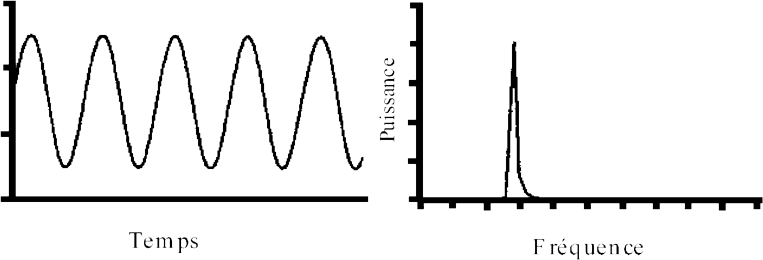
Un autre signal avec une fréquence plus aigu :
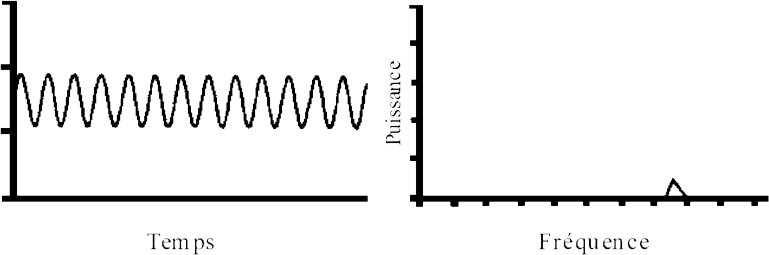
En additionnant les 2 signaux, nous obtenons un spectre de raies qui contient ces 2 fréquences puisque qu'il s'agit de 2 sinusoïdes pures qui ne contiennent pas d'harmoniques.
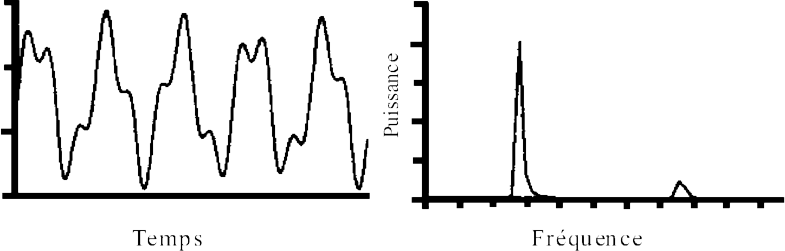
Dans le cas d'un spectre continu, comme celui d'un bruit, du vent ou d'une simple impulsion, si nous décomposions ce son, c'est-à-dire en appliquant la transformée de Fourier (FFT), nous obtiendrions un spectre continu.
Les sons complexes quelconques : transformée de Fourier rapide (Fast Fourier Transform)
La transformée de Fourier est l ’outil mathématique permettant de connaître et représenter le spectre de n'importe quel signal dans une fenêtre temporelle donnée.

Cette fenêtre temporelle est très importante a déterminer sur n'importe quelle mesure pour analyser correctement ce que l'on veut observer sur notre spectre.
Le meilleur exemple est lorsque l'on veut faire la FFT d'une réponse impulsionnelle. La courbe de réponse (le spectre) varie en fonction de la fenêtre de mesure. Un autre exemple est sur les analyse de spectre en temps réel qui ont aussi une fenêtre de mesure qui peut être glissante ou automatique mais elle est prise en compte pour le calcul.
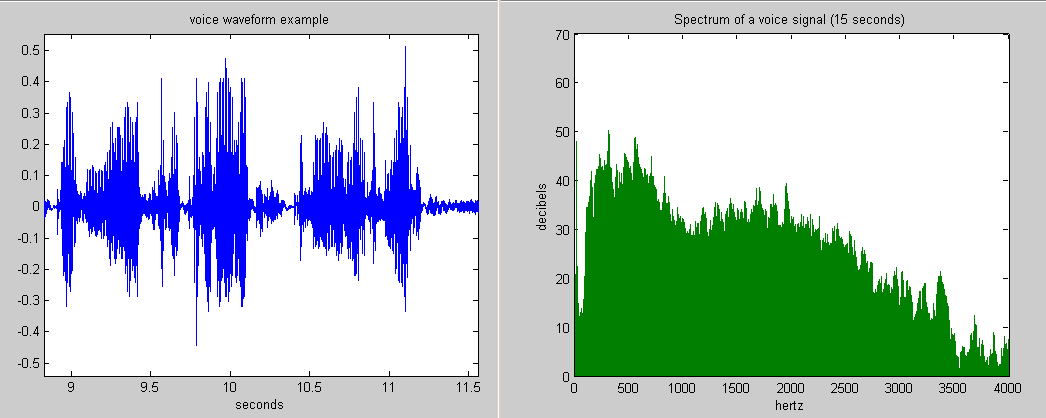
Ici l'analyse fréquentielle d'une voix sur une durée de 15 secondes.
Le timbre musical
Le timbre d'un son est défini par les rapports d’amplitude, temporels et fréquentiels entre les composantes du signal audio.
Contrairement à une sinusoïde pure, le timbre d'un son est caractérisé par un mélange de plusieurs sons différents. Il y a d’abord ce que l ’on appelle la fréquence fondamentale (qu’on appelle aussi le premier harmonique), qui définit la hauteur du son (grave, médium, aigu ou dans des cas précis une note d’une certaine hauteur) et naturellement, il se complète d'une multitude d’autres harmoniques. Il s’agit en fait de multiples, pairs et impairs de la fondamentale, dont le volume décroît au fur et à mesure.
Ce sont ces harmoniques qui sont responsables de la couleur du son, et c’est cela qui nous indique si l’instrument est un saxophone ou un piano, une guitare ou même une voix d’homme ou de femme, même s’ils émettent exactement la même note (fréquence f)
Il sera également défini par le profil dynamique d’un son qui va se déterminer de manière temporelle.





