Les ondes sphériques
Une onde sphérique est une onde dont les fronts d'onde sont des sphères. On parle aussi de source isotrope, c'est a dire qu'elle emet le même son dans toutes les directions. Pour visualiser ce qu'est une onde sphérique, imaginer un moustique qui est une petite source sonore qui evolue dans un très grand espace autour sans aucun obstacles autour de lui. Il emet donc autant de son devant derrière en haut bas en bas qui crée donc une sphére.
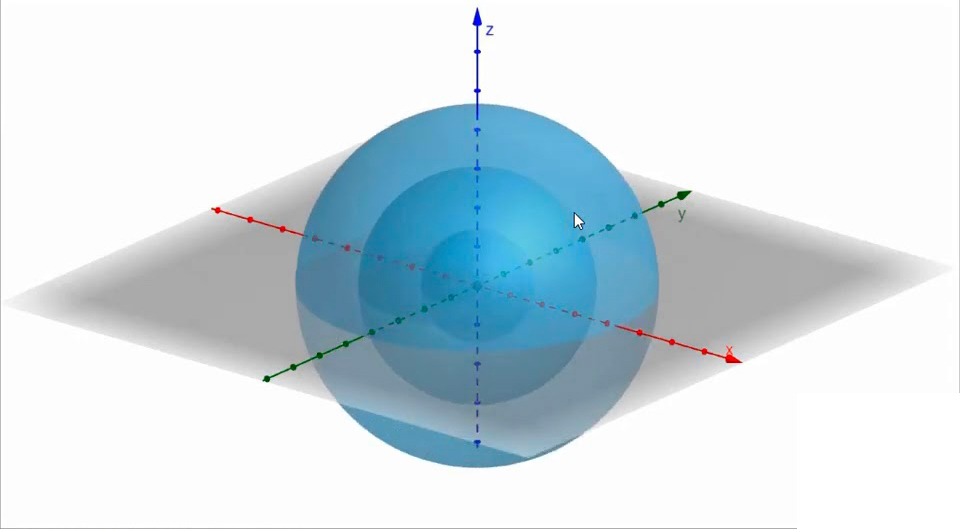
Le front d'onde va se developper et créer une sphére de rayon (r) puis le niveau se dissipera petit à petit sur une surface de plus en plus grande.
Mathématiquement nous pourrions calculer la puissance acoustique (Wa) ou l'intensité acoustique (Ia) de notre source sonore sur une surface donnée en m2, en appliquant cette formule :
Wa = Ia . 4 pi r2
Ia = Wa / 4 pi r2
Ia c'est l'intensité acousitque qu'il y a sur 1 m2 de surface correspondant au rayon (r).
4 pi r2 surface d'une sphére.
La puissance acoustique reste constante, puisqu'il s'agit de notre source sonore. Plus on augmente le rayon de cette sphère (r) plus l'intensité acoustique (Ia) diminue. Ce qui explique pourquoi le niveau diminue quand on s'éloigne d'une source.
Pour avoir des valeurs en db, nous pouvons appliquer ces formules :
LW = LI + 10 log(4πr2)
LI = LW ‐ 10 log(4πr2)
De ce point de vue là, cela ne nous parle pas beaucoup pourtant c'est un principe que nous appliquons quotidienneenment dans nos séances de prises de son. Ces calculs explique la décroissance de 6db lorsque que l'on double la distance à la source.
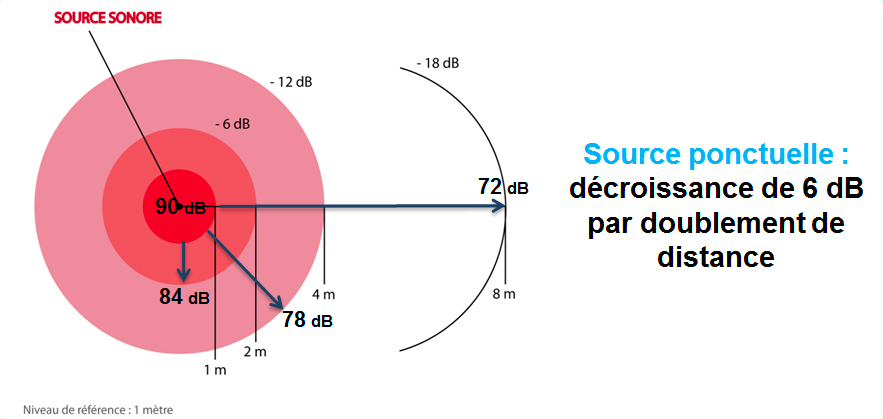
Pour expliquer d'un point de vue mathématique, en doublant la distance c'est comme si on multipliait par 2 notre rayon. Or sur notre formule cela deviendrait :
LW = LI + 10 log(4π 2r2)
On passe de r2 à 2r2, Cela rajoute un 2 au carré sur la multiplication. Avec les logs, log ab = log a + log b c'est à dire que le log d'une multiplication devient la somme des 2 logs.
Donc nous avons 10log (2 x 10log (4π r2)) qui donne (10log 22 +10Log 4π r2) et comme un Log a2 = 2log A ca devient : (10Log 4π r2+20log2) 20 log 2 = 6db (6,02 pour être précis)
Prenons un autre exemple avec une source sonore sphérique avec un niveau de pression de 90 dbSPL mesuré à 1m, quels serait son niveau de puissance acoustique ?
- Lw = LI + 10 log(4π r2)
- Lw = 90 + 10 log(12.5 x 1)
- Lw = 90 + 10 x 1,1
- Lw = 90 + 11
- Lw = 101 dB





