Caractéristiques du signal acoustique d’un son pur
Dans l’article précédent, nous avons vu que la variation d’intensité acoustique se traduit par un mouvement vibratoire représentable sous forme de sinusoïde.
Un son pur correspond précisément à ce mouvement sinusoïdal, que l’on peut représenter de la manière suivante :
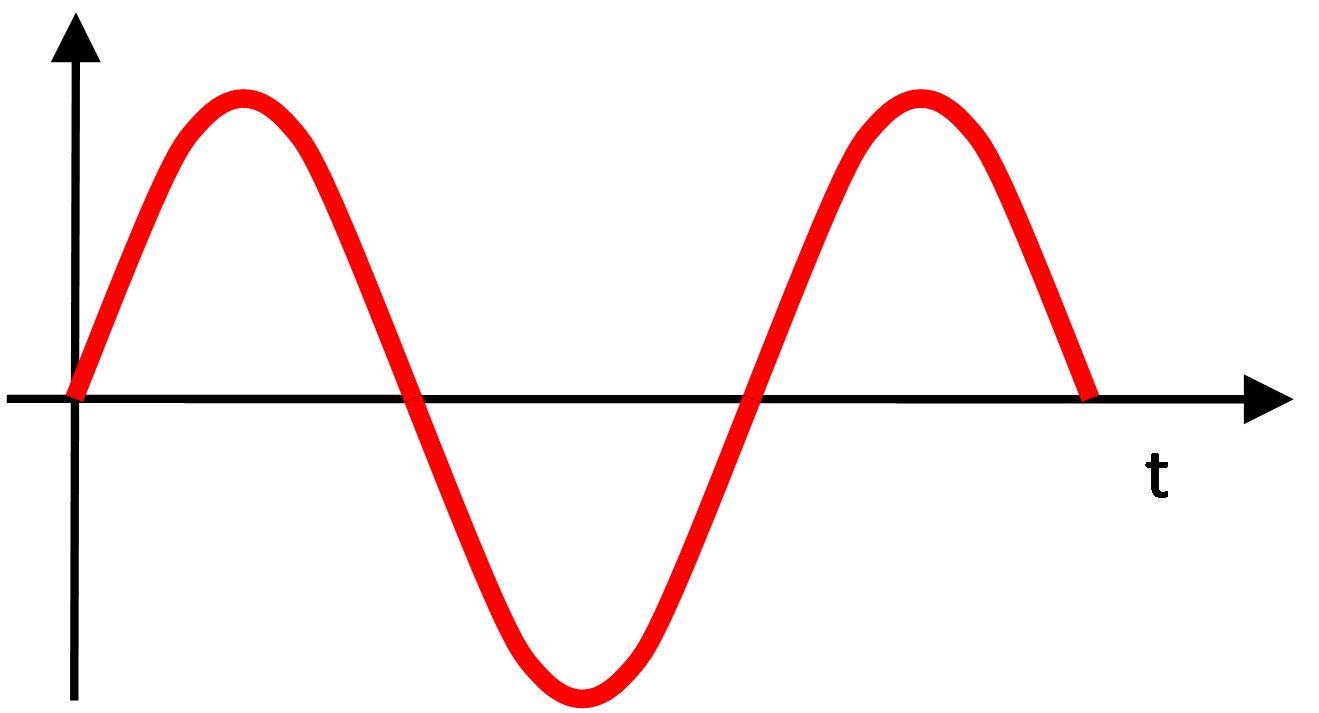
Une sinusoïde est définie par son amplitude, exprimée en pression (ou en tension). Mathématiquement, elle s’écrit :
p = pmax . sin(ωt)
- p : pression instantanée
- pmax : pression maximale
- ω : pulsation (vitesse angulaire)
La période T définit la durée d'une période (en secondes). Pendant cette période, la sinusoïde :
- part de 0,
- atteint une valeur maximale,
- revient à 0,
- atteint une valeur minimale,
- revient à 0.
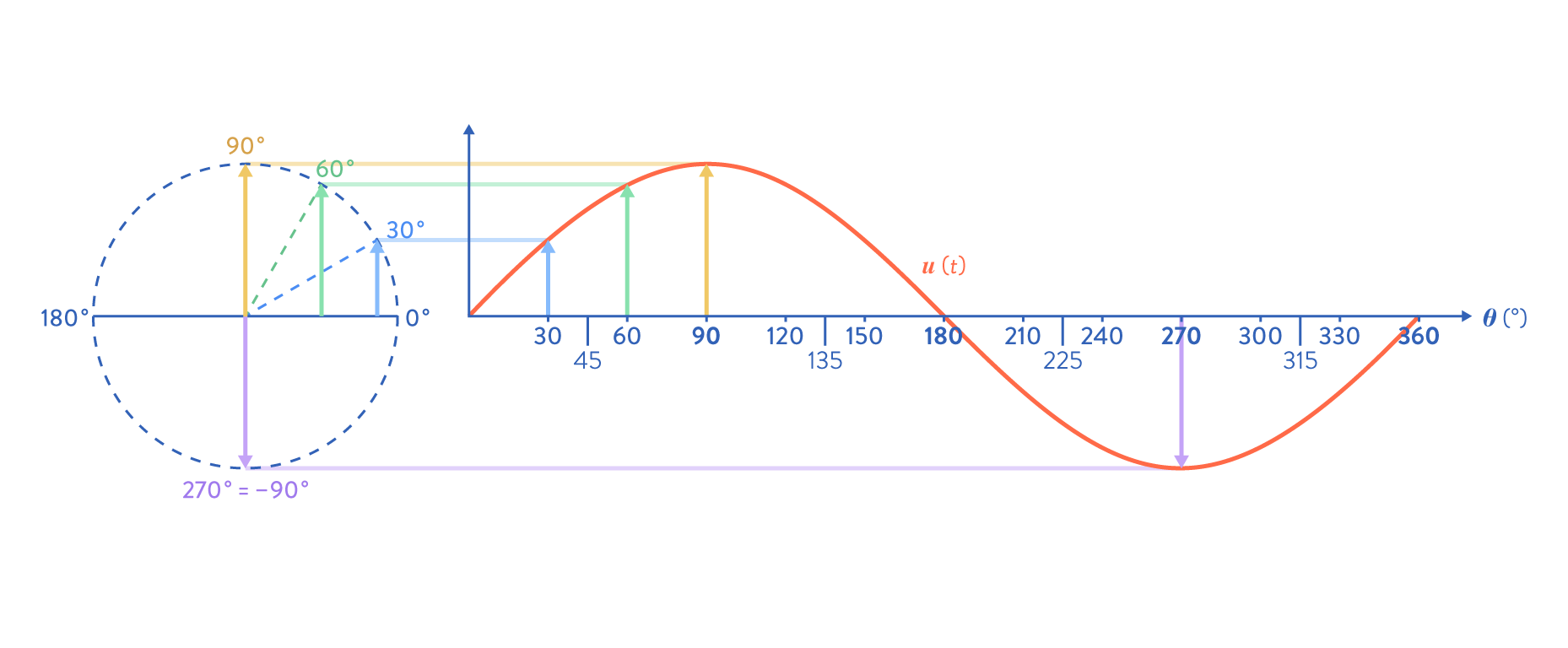
La vitesse à laquelle ces cycles se répètent est appelée pulsation (ω) ou vitesse angulaire. Une rotation complète correspond à 360°, soit 2π radians.
ω = pulsation (rd/s) = vitesse angulaire = 2π / t
‐1 ≤ sin(ωt) ≤ +1
Définition générale de la sinusoïde
Une sinusoïde est mathématiquement définie par :
U(t) = U0 cos(Ωt+Ø) (période)
Ω = 2 πf (fréquence)
- U0 : amplitude du signal en tension par exemple
- Ω=2πf : pulsation
- f : fréquence du signal (Hz)
- Ø : phase du signal (rd)
La sinusoïde est caractérisée par son amplitude A et donc sa fréquence f et la période T définit la durée du cycle (en secondes).
La fréquence et la période sont donc liées par la relation f = 1/T donc T = 1/f
Ex : 1Hz = 1 cycle par seconde
440Hz = 440 cycles par seconde et donne la note LA standard.
Si une sinusoïde a pour période T = 5ms, alors f=1/0,005=200 Hz
Phase mathématique entre 2 signaux
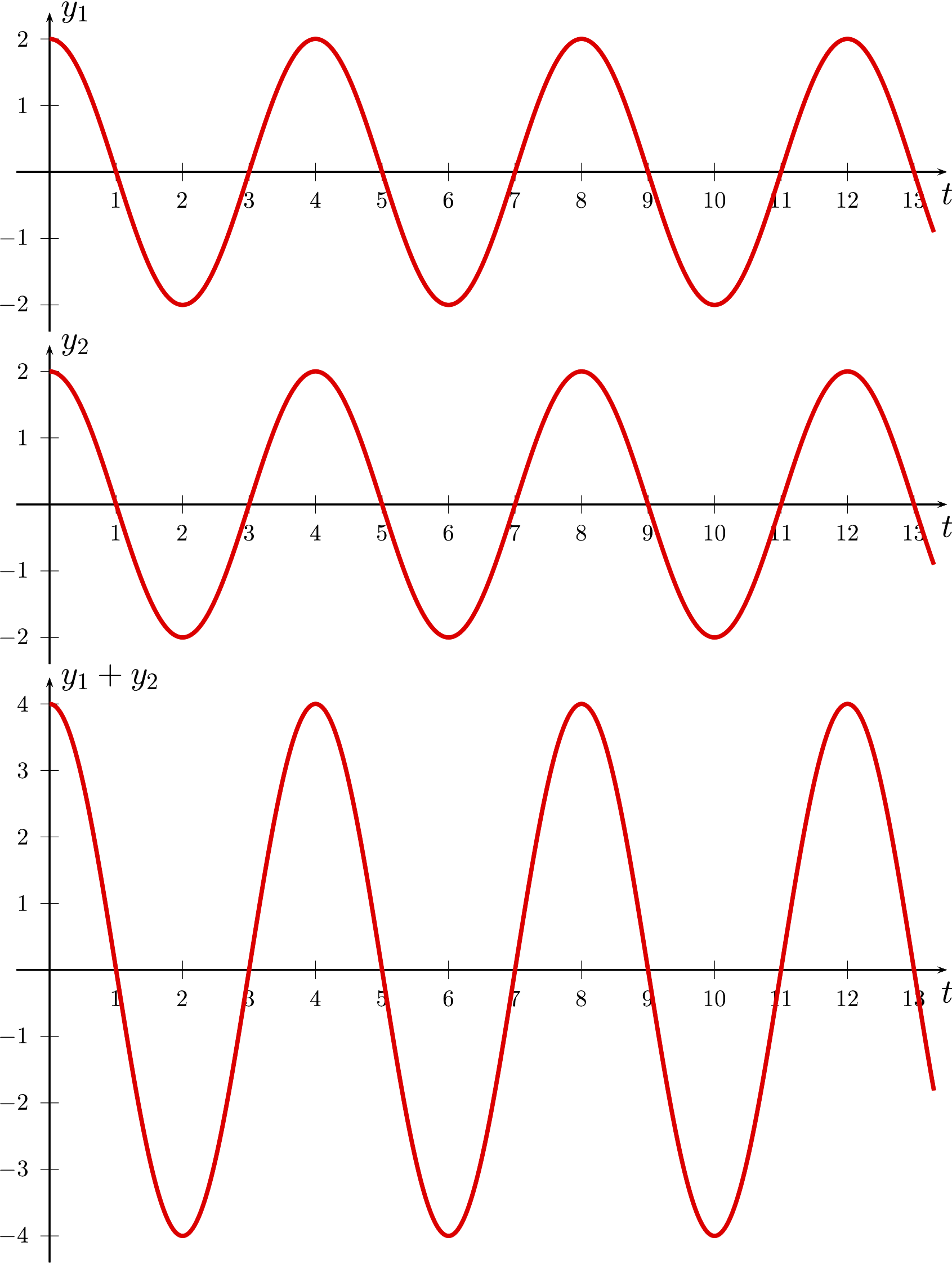
Voici 2 signaux (y1 et y2) parfaitement superposés, nous dirons que ces signaux sont "en phase". Par conséquent, ils s'additionnent en niveau.
Ø = 0
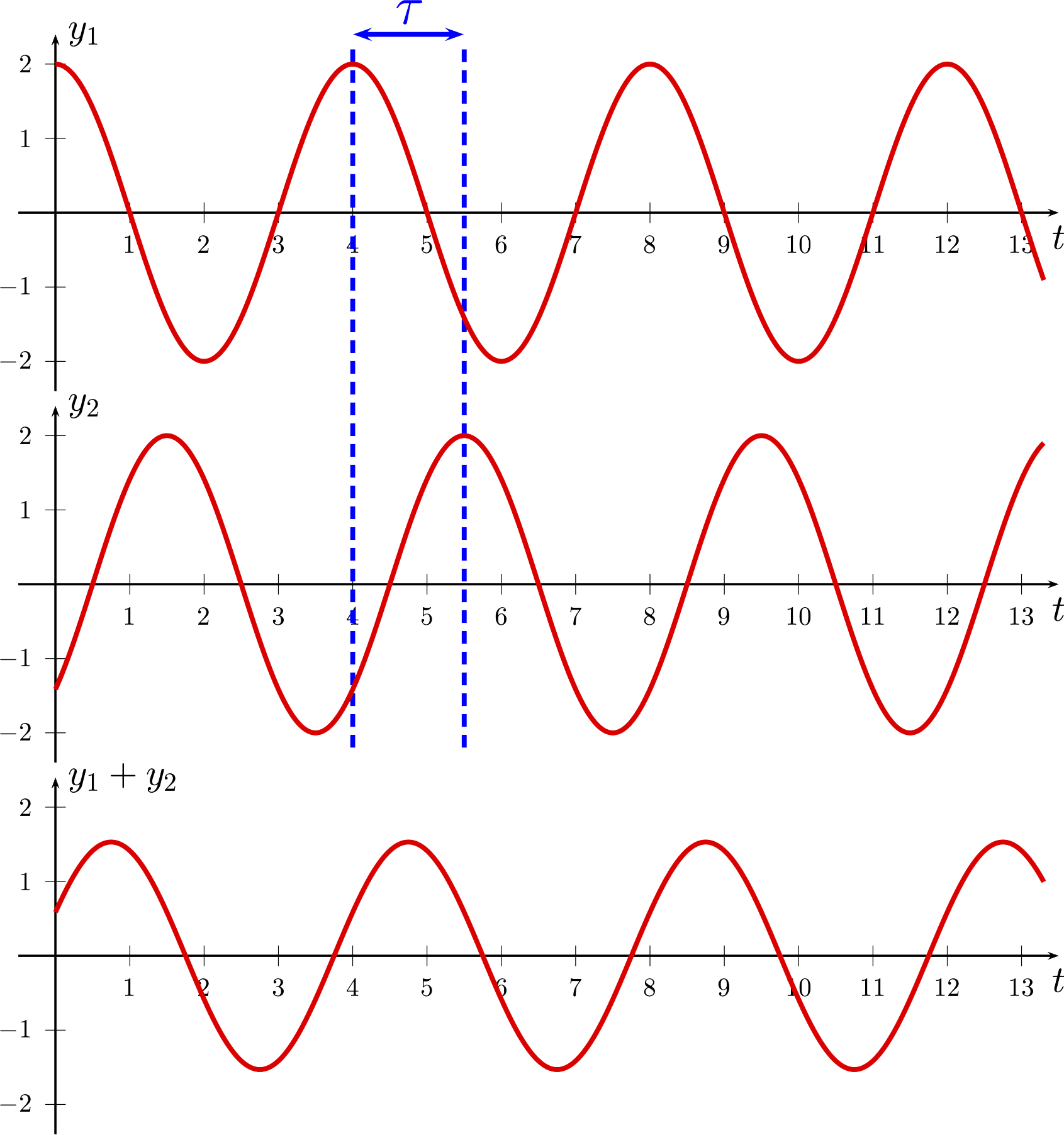
Nos 2 mêmes signaux en quadrature de phase, la y1 démarre à 90° tandis que y2 démarre aux alentours des 270°. L'addition des 2 signaux modifie le timbre d'origine du signal.
Ø = Ω / 3
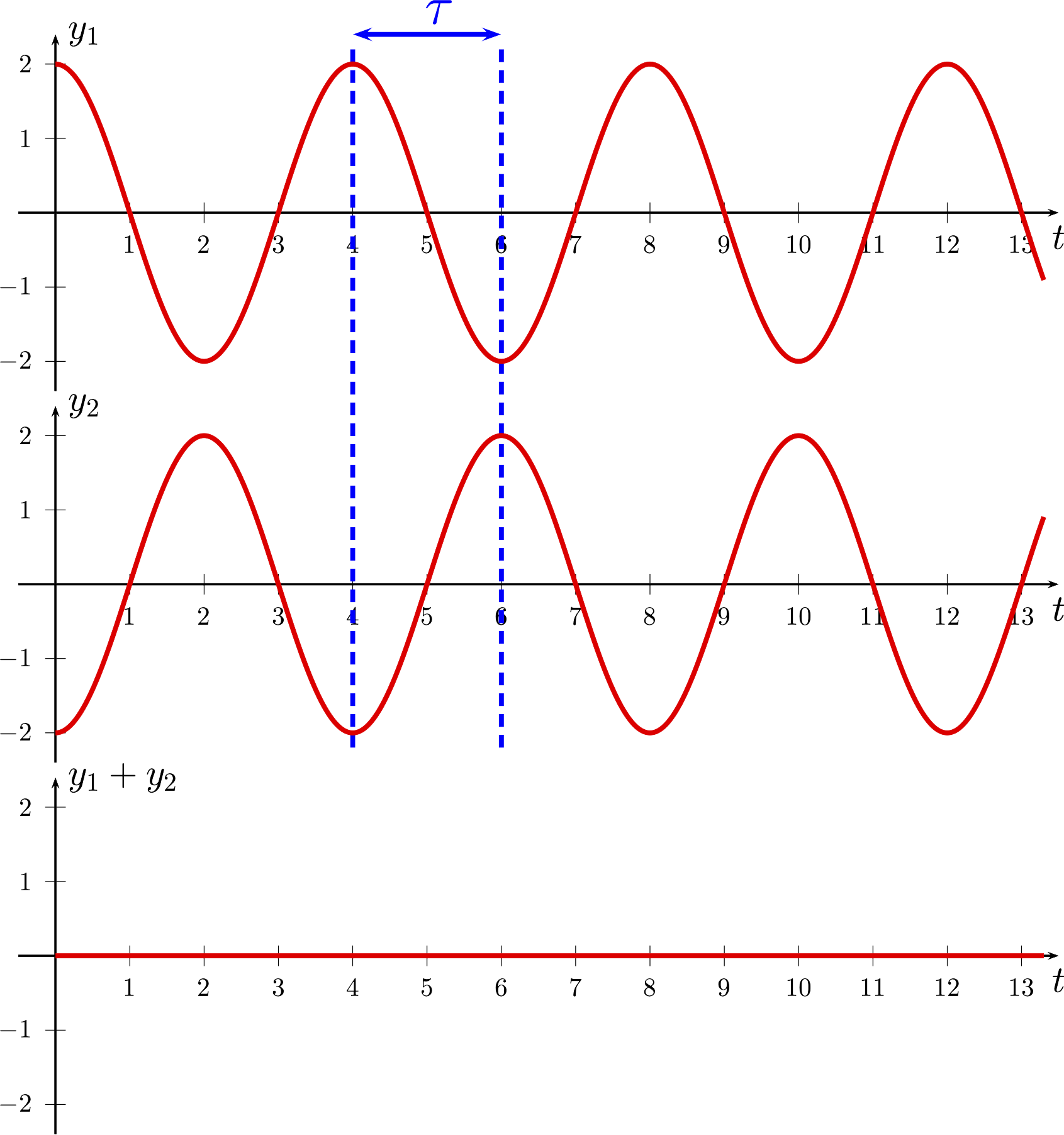
Nos 2 signaux en opposition de phase (on parle de polarité inversée). Dans ce cas, les signaux s'annulent.
Ø = Ω
Longueur d'onde
La longueur d'onde (λ) se mesure en mètre et correspond au développement dans l'espace de propagation d'une période T (s). C'est aussi une distance qui correspond à une fréquence f (Hz).
λ = c . T
λ = c / f
c correspond à la célérité du son qui est la vitesse de déplacement de l'onde sonore qui est égal à 340 m/s (dans l'air à 15°C)
Il ne faut pas confondre la vitesse vibratoire d'une molécule qui est liée à la fréquence et la vitesse de propagation.
Un son d’une fréquence de 1000 Hertz, par exemple, ondule donc 1000 fois en une seconde, on peut très simplement calculer la longueur d’onde, qui serait de 34 cm. On peut calculer la longueur d’onde du son audible le plus grave, par exemple 20 Hz qui serait dune longueur de 17 mètres et du son le plus aigu (disons de 20kHz) qui serait de 17 millimètres.
f = 20 Hz ↔ λ = 17 m (T = 50 ms)
f = 1 kHz ↔ λ = 34 cm (T = 1 ms)
f = 20 kHz ↔ λ = 17 mm (T = 0.05 ms)
Il est important de prendre l'habitude de rapporter ces longueurs d'onde aux objets qui nous entourent pour appréhender l'impact acoustique qu'ils peuvent avoir. Prenons l'exemple d'un écran d'ordinateur qui aura un impact sur le médium aigu mais aucun sur les fréquences graves.
Prenons un autre exemple comme un paravent acoustique d'une dimension D, il jouera un effet d'obstacle.
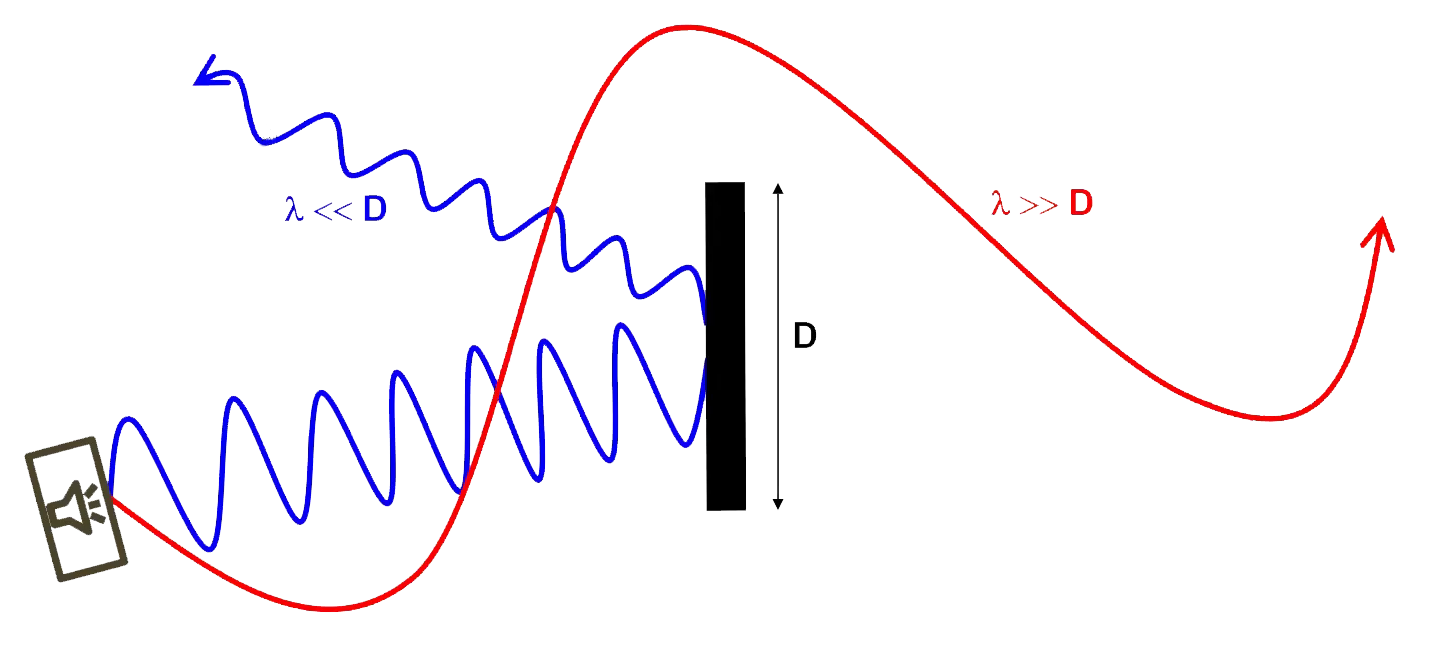
Pour les petites longueurs d'ondes (fréquences élevées) le paravent bloquera ces fréquences. Elles seront réfléchies ou absorbées en fonction de la composition du panneau. En revanche, pour les longueurs d'ondes plus longues (fréquences graves) le paravent sera complètement "transparent" sans aucune incidence sur ces fréquences.
La sensation de hauteur de son
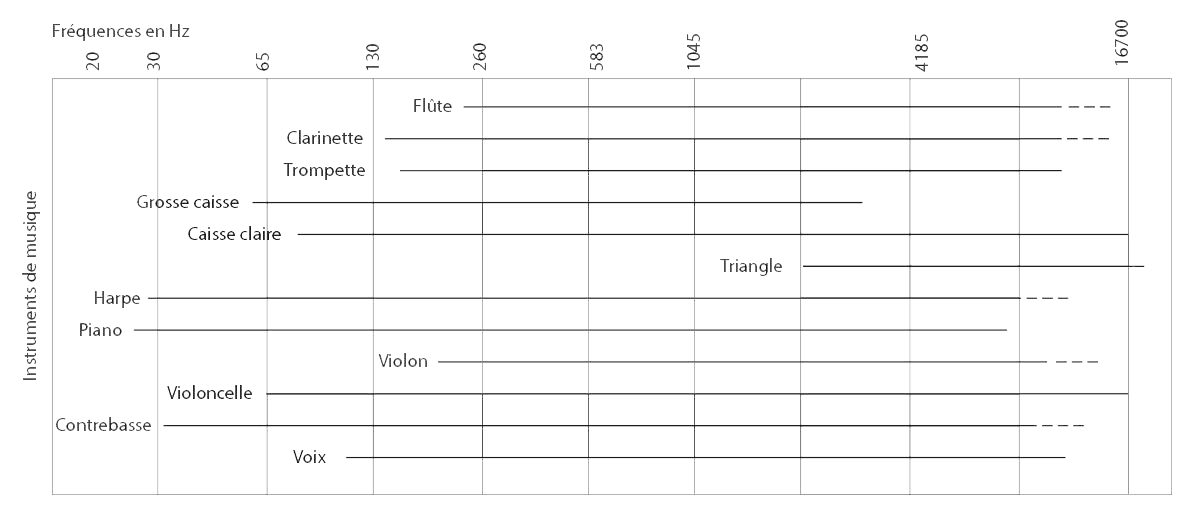
En physique nous parlons de fréquence mais en musique on pourrait parler de tonie avec la référence que l'on connait tous, à savoir un la qui correspond à la fréquence de 440Hz.
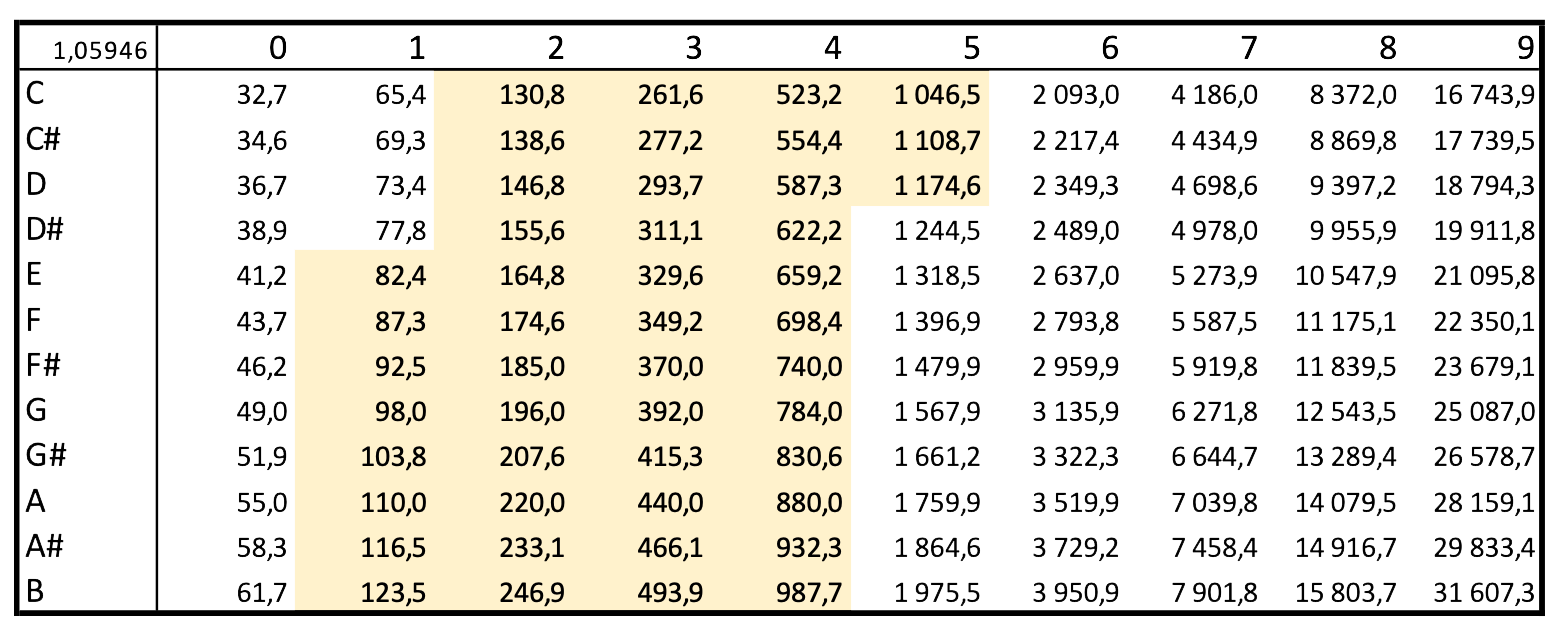
Dans ce tableau vous avez différents exemples de la tessiture d'instruments de musique. Cela inclut les fréquences fondamentales sans les harmoniques.