Les différents types de décibels (db)

Les décibels ou db sont l’unité par excellence dans le monde l’audio. Celle ci permet d’exprimer le rapport entre deux grandeurs, entre une grandeur et une référence, un gain en tension, en puissance… Les décibels résultent du logarithme du rapport de deux grandeurs. 

Lorsque les électro-acousticiens se sont intéressés à l’analyse des phénomènes acoustiques, il leur a fallu définir une échelle évoluant d’une manière approchant la variation de notre perception. Cette unité a été créée dans le but de simplifier les calculs, ou plus simplement de comprimer l’énorme étendue de l’échelle des intensités sonores audibles par un être humain par exemple.

C’est Alexander Graham Bell, physicien américain né à Edeibourg en 1847, l’un des inventeurs du téléphone, à l’origine professeur pour sourds et muets, qui a établi la première échelle de mesure acoustique, il s’agissait alors du Bell.

Son analyse portait sur le fonctionnement de l’oreille, il a choisi une fréquence de référence : 1000 Hz (fréquence pour laquelle l’échelle des phones évolue de façon géométrique et régulière) conservée depuis lors par les électro- acousticiens et les preneurs de son comme fréquence de référence.

A cette fréquence, il a, dans un premier temps, évalué le seuil de l’audibilité, en prenant un panel suffisamment large de population. En suite, il a fait une moyenne pour savoir quel était le niveau de perception minimal d’un signal acoustique de 1000 Hz.

Le résultat obtenu était de 10^-12 W.m^-2. Puis il a évalué le niveau acoustique maximum acceptable par l’oreille. Il a trouvé une valeur de 10 W.m^-2. Cela s’étend donc de 10^-12 W.m^-2 à 10² W.m^-2….

A partir de ces valeurs qui constituent la dynamique absolue de l’oreille à 1000 Hz, c’est à dire la différence de niveau entre la plus petite intensité acoustique audible et la plus forte supportable, il a établi une échelle de comparaison en prenant comme référence la plus petite intensité acoustique audible à 1000 Hz.

Le Bell acoustique est égal à : Niveau en Bell = log I / I₀

I est l’intensité acoustique mesurée et I₀ est l’intensité acoustique de référence (seuil de l’audibilité à 1000 Hz) = 10^-12 W.m^-2.

Si on applique ces valeurs minimale et maximale à cette loi de variation on obtient :

log I₀ / I₀ = 0 Bell

log I max / I₀ = log 10²/10^-12 = 14 Bell.

On s’aperçoit alors qu’on est passé d’une échelle linéaire allant de 10^-12 W.m^-2 à 10 W.m^-2 à une échelle logarithmique sans dimension (puisqu’il s’agit d’un rapport) ayant 14 intervalles. Cette nouvelle échelle manquait de précision. Il a suffit de multiplier la fonction par 10 pour obtenir 10 fois plus de précision. Chaque intervalle représente le 1/10 de l’intervalle du Bell, d’où le décibel (dB) :

Niveau en dB = LI = 10 log I / I₀

L’échelle devient :

LI min = 10 log I₀ / I₀ = 0 dB

LI max = 10 log I max / I₀ = 10 log 102/10-12 = 140 dB

L’échelle des intensités acoustiques en dB contient donc 140 intervalles.

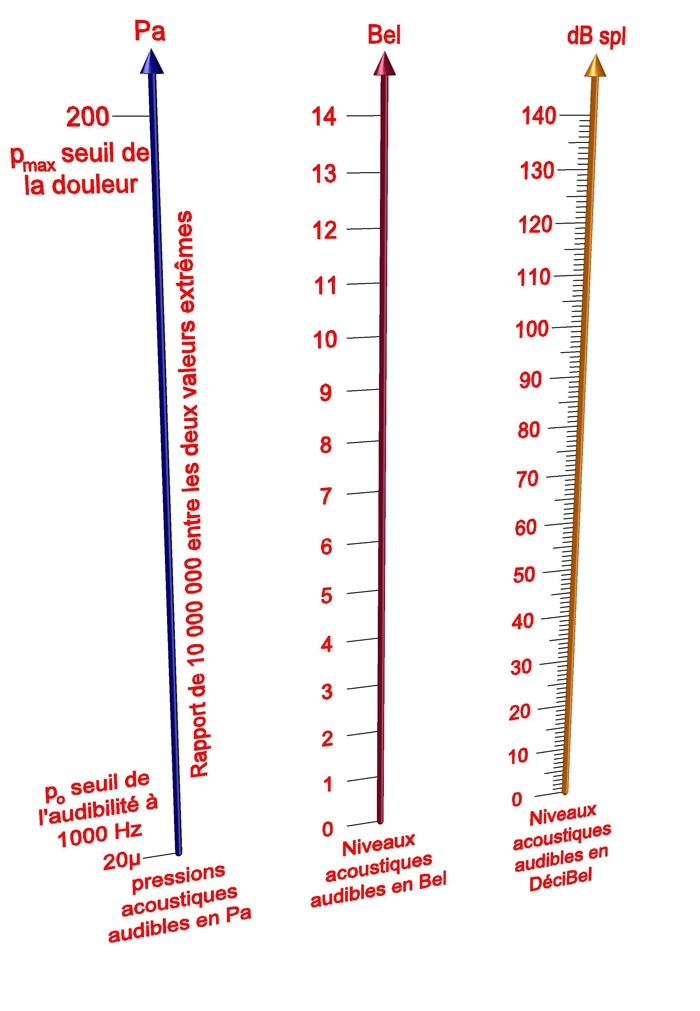
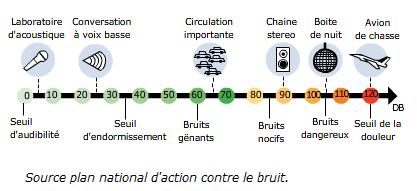
En décibels, cela donne une échelle de 0 à 140 dB, 0 dB correspondant au seuil d’audition et 140 dB au seuil de douleur. Largement plus simple d’utilisation que nos W/ m² !

Et lorsqu’on se base sur une grandeur de référence, cela va permettre de calculer une valeur absolue.

Le décibel est utilisé comme mesure du rapport entre deux puissances dans certains domaines, comme les télécommunications ou le radar pour décrire des gains ou des amplifications (dB positifs) ou des pertes ou des atténuations (dB négatifs). On parle alors d’une atténuation de 15 dB compensée par un amplificateur avec 15 dB de gain. Une atténuation de 15 dB est équivalente à un gain de -15 dB.

Le décibel a donné naissance à un certain nombre d’unités (sans dimensions) utilisées pour mesurer des puissances ou des intensités de façon absolue. Ceci se fait en utilisant comme puissance de référence (dans le dénominateur de la définition précédente) une valeur de puissance prédéfinie. Dans ce cas, on ajoute une lettre à « dB » pour savoir de quoi on parle.

Les différents types de db

dB SPL : décibel en acoustique

Le dBSPL (ou dB SPL) = decibel Sound Pressure Level, est utilisé dans le domaine de l’acoustique, plus précisément là où il est question de pression acoustique. L’utilisation d’une telle unité présente un grand interêt en acoustique car la sensation auditive que l’on éprouve à l’audition d’un son est proportionnelle au logarithme de l’excitation.

Comme pour les Watts et les Volts, l’usage d’une référence est nécessaire. Cette référence est le seuil d’audibilité de l’oreille humaine, c’est à dire le niveau sonore au-dessous duquel l’oreille n’entend plus rien. Comme nous l’avons vu plus haut, le seuil d’audibilité pour un son à 1 kHz, a été « fixé » (moyenne reconnue pour un ensemble donné d’individus) à 10^-12 Watt/m².

La puissance acoustique ainsi exprimée en décibel sera ainsi directement en rapport avec la sensation éprouvée lors de l’écoute. Si P exprime la puissance sonore émise et si Pr exprime la puissance sonore de référence (seuil d’audibilité), alors l’écart entre ces deux puissances peut s’écrire selon la formule suivante :

Ecart = 10 log (P / Pr)

Ainsi, le niveau sonore à 1 kHz est défini par la formule suivante :

Psonore = 10 log (P / 10^-16)

Comme l’oreille est un capteur de pression acoustique (seule la face externe du tympan est soumise à l’influence de la pression acoustique, comme les microphones omnidirectionnels), il est plus commun d’exprimer le dB acoustique en fonction de la pression acoustique et non de l’intensité acoustique :

La loi d’Ohm appliquée à l’acoustique nous donne I = p2 / Z.

I l’intensité acoustique (grandeur semblable à la puissance électrique) exprimée en W.m-2 (puissance surfacique).

p la pression acoustique (grandeur semblable à la tension électrique) exprimée en Pascal.

Z l’impédance acoustique (grandeur semblable à l’impédance électrique) exprimée en rayls. Z = r0 c

Si on remplace dans l’expression : LI = 10 log I/I0

LI = 10 log p2 / Zp02 / Z0 = 10 log p2 / p02

et donc

LI = Lp = 20 log p / p0. (Rappel : log ax = x log a)

On peut simplifier par Z car l’impédance ne change pas en fonction du niveau : L’impédance caractéristique de l’air Z0 = 400 rayls (propagation en champ libre).

Et p0 = 6 (I0.Z0) = 2.10-5 Pa.

p0 = 2.10-5 Pa.

Le dBSPL (Sound Pressure Level) = Lp = 20 log p/p0.

Lorsque vous lisez les documentations sur vos microphones, vous verrez la pression maximale qu’ils peuvent supporter. C’est une valeur exprimée en db SPL.

Le dBu

Le dBu s’appelait auparavant dBv, unité qui a été transformée pour éviter toute confusion avec l’unité dBV. Le dBu est une unité utilisée pour quantifier l’amplitude d’un signal électrique, et son usage en audio est très fréquent. Le dBu mesure la tension par rapport à une référence de 0,775 volts RMS. Cette valeur de référence correspond à la tension d’une charge de 600 ohms soumise à 1 mW.

Pour les électro-acousticiens et les preneurs de son, la grandeur image de la pression acoustique est la tension, car les sorties d’amplificateurs sont en basse impédance et les entrées en haute impédance; il n’y a donc pas d’adaptation en puissance. Le dBm n’a donc pas de raison d’être.

Néanmoins, la référence en tension se calque sur la référence en puissance à 1 mW. Sachant que l’impédance caractéristique des lignes PTT est de 600 W, il vient :

P0 = U02/R U0 = 6(P0.Z)

U0 = 6 0.6

U0 = 0.775 V

C’est la référence du 0 dBu et niveau en dBu = 20 log U/U0.

Le matériel audio professionnel travaille généralement au niveau électrique de +4 dBu, soit 1,228 V (ou 1,78 dBV)

Le dbm

Comme il fallait bien transporter électriquement les modulations, images de l’intensité acoustique, on était confronté aux mêmes dynamiques que celles de l’acoustique. Il était alors simple de prendre une échelle d’évolution des niveaux électriques identique à celle de l’échelle acoustique mais dont la référence serait établie de façon arbitraire (il aurait été difficile de choisir un zéro dB électrique en fonction d’une perception sensitive, peut être celle de la chaise électrique !!!).

Le premier dB électrique de référence fut celui du téléphone défini pour une puissance de référence de 1 mW, il s’agit du dBm.

Et le niveau en dBm = 10 log P / P0.

Le 0 dBm correspond donc à un niveau de 1 mW sous 600Ω (soit 0,775V). Il est employé pour les transmissions en puissance, (adaptation d’impédance Zs = Ze) quelle que soit l’impédance de la ligne. La mesure effectuée en dBm sous 600Ω est identique à la mesure effectuée en dBu. Remarquez que la valeur de la puissance dissipée (1 mW) du dBu est la même que celle qui à conduit au choix de la référence du dBm, sauf que la résistance n’était pas de 600 ohms, mais de 50 ohms.

dBV

Le dBV mesure la tension par rapport à une référence de 1 volt RMS. Le matériel audio grand-public travaille généralement au niveau électrique de -10 dBV, soit 0,3162 V (ou -7,78 dBu)

Une tension de 1 Veff correspond à 2,21 dBu. Comme il semblait plus logique d’utiliser une référence plus « normale » pour une tension, la valeur de tension 1Veff a été retenue pour servir de référence à une nouvelle unité : le dBV (avec un V majuscule). Notez la différence d’unité du volt entre dBu et dBV : 1 Vcac pour 0 dBu et 1 Veff pour 0 dBV.
dBV = 20 log (U / 1) soit dBV = 20 log (U)

Attention à ne pas confondre dBu et dBV, la différence est subtile mais existe ! Prenons l’exemple d’une tension de 10 Volts. Avec les formules précédentes, nous obtenons 22,2 dBu et 20 dBV… Ce n’est pas la même chose ! Remarquez que certains systèmes de mesure de niveau audio affichent seulement l’unité « dB ». Pas facile de s’y retrouver dans ce cas là.

Infos provenant du site : www.sonelec-musique.com

Rapports dB analogiques

0,775V = 0 dBu = 0 dBm

1V = 0 dBV =  = +2,2 dBu

Niveau vu-mètre 0 VU = +4 dBu = 1,228 V = +1,78 dBV

dB numérique dbFS

dBFS = decibel Full Scale (Full Scale = pleine échelle). Valeur de référence = 0 dBFS = maximum d’amplitude permise avant écrêtage du signal.

Le dBFS n’est utilisé que dans le domaine numérique, le terme FS signifiant Full Scale et se référant à l’échelle maximale de valeurs que peut traiter le système numérique. Il est donc impossible de spécifier une valeur analogique universelle comme référence. On peut très bien se trouver face à un appareil numérique doté d’entrées et de sorties analogiques (une console de mixage ou un convertisseur A/D-D/A par exemple), pour lequel le 0 dBFS correspond à une valeur arbitraire fixée par le fabricant. Chez l’un, on pourra lire que le 0 dBFS correspond à une amplitude de 0 dBu à l’entrée du convertisseur A/D, chez un autre, on pourra lire que le 0 dBFS correspond à une amplitude de -10 dBu à l’entrée du convertisseur A/D. En général ces valeurs tournent autours de -18, -16dbu. Il est tout de même important de savoir à quels niveaux on doit travailler en entrée et en sortie d’un équipement numérique et si vous possédez plusieurs convertisseurs avec des valeur différentes, il faudra être capable de les calibrer à la même valeur.

Rapports dB analogique/numérique

En Europe : -18 dB fs <=> +4 dBu

Aux USA : -20 dB fs <=> +4 dBu

Radio : -16 ou -14 ou -12 dB fs <=> +4 dBu

Le dBu0s

Ce dB particulier est utilisé uniquement dans les circuits de modulation broadcast (radio télévision). Son utilisation exprime qu’il s’agit d’un niveau d’alignement adapté à chaque utilisateur de la chaîne audiofréquence broadcast.

Cette notion de signal d’alignement est intéressante dans la mesure où il n’est pas nécessaire de préciser le niveau de tension de ce signal. En effet, il suffit d’annoncer que le circuit de modulation est alimenté par un signal d’alignement 0 dBu0s et chaque utilisateur, tout au long de la chaîne audio, se règle sur son propre niveau de travail. C’est le cas, par exemple, des niveaux d’alignement entre le studio de production (+4 dBu) et les lignes de transmission internationales (+6 dBu).

Le dBu0s signifie qu’il s’agit :
d’un niveau absolu de tension référencé à l’échelle des dBu, d’un signal de test sinusoïdal d’une fréquence de 1000 Hz (0), d’un circuit de transmission audiofréquence broadcast.

Le dB :

Le dB sans qualificatif exprime le rapport entre deux grandeurs de même nature, qu’elles soient acoustiques ou électriques. Il s’écriera ainsi :

Le niveau en dB = 20 log R

R est le rapport entre les deux grandeurs que l’on souhaite comparer. Dans cette expression, « 20 log » nous indique qu’il s’agit de la comparaison de pression, tension ou courant. Dans le cas des grandeurs énergétiques, on utilisera la relation 10 log R.

On trouve désormais la désignation dBrs. Cette écriture exprime la même chose que le dB sans qualificatif. La qualification « rs » signifie « relatif signal » au sens de la tension et non de la puissance.

1er cas : Pour une augmentation ou une diminution d’un même signal exprimé en pression, en tension ou en courant, il vient :

• une multiplication par 2 donne un gain de +6 dB,
• une division par 2 donne une atténuation de -6 dB,
• une multiplication par 10 donne un gain de +20 dB,
• une division par 10 donne une atténuation de -20 dB.

2ème cas : Pour une augmentation ou une diminution d’un même signal exprimé en puissance électrique ou en intensité acoustique, il vient :

• une multiplication par 2 donne un gain de +3 dB,
• une division par 2 donne une atténuation de -3 dB,
• une multiplication par 10 donne un gain de +10 dB,
• une division par 10 donne une atténuation de -10 dB.

3ème cas : addition de signaux exprimés en pression, en tension ou en courant de mêmes niveaux n’ayant aucune corrélation entre eux, il vient :

• l’addition de 2 signaux donne un gain de +3 dB,
• l’addition de 10 signaux donne un gain de +10 dB.

C’est le cas du mixage multipiste.

Pour résumer…

Rappelez-vous simplement qu’un gain (+40 dB par exemple) ou une atténuation (-20 dB par exemple) ne désigne aucune valeur absolue, mais une différence (ou un rapport) entre deux valeurs. Pour désigner une valeur absolue, il faut ajouter la petite lettre qui va bien après le dB (+12 dBu par exemple). Il existe donc le dB, le dBm, le dBu et le dBv…

Un grand merci à Gilles Serin pour le complément d’informations.